Electronic And Circuit Diagram

A set of impedances are connected in parallel when "all of them are subjected to the same voltage", unlike the series impedances where all of them are crossed by the same current.

The equation for each of the impedances in parallel is

u1 = Z1⋅i1; u2 = Z2⋅i2, u3 = Z3⋅i3 ... un = Zn⋅in

In addition, equality is also fulfilled

u1 = u2 = u3 = ... = un = u

 Resistors in parallel and Intensity Divider

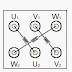
 Parallel impedance association

 By applying the first Kirchhoff law to the impedance association in parallel you get
i = i1 + i2 + i3 + ... + in = u1Z1 + u2Z2 + u3Z3 + ... + unZn

Since the voltage applied to all the impedances is the same for all of them, it results
i = (1Z1 + 1Z2 + 1Z3 + ... + 1Zn) ⋅u

If the parallel association of impedances was equivalent to a single impedance (Zeq = Zparallel), applying Kirchhoff's law would result

i = uZparallel

Comparing both expressions, it is concluded that
1Zparallel = 1Z1 + 1Z2 + 1Z3 + ... + 1Zn

If all the impedances in parallel were resistors, it would be obtained that
1Rparallel = 1R1 + 1R2 + 1R3 + ... + 1Rn

Analogously, if all the impedances were coils without coupling, one would obtain
1Lparallel = 1L1 + 1L2 + 1L3 + ... + 1Ln

In the case that all the impedances were capacitors, we have
Cparallel = C1 + C2 + C3 + ... + Cn

In addition to obtaining the equivalent parallel impedance, it is also important to establish the relationship between the intensity of each of the impedances that make up the equivalent parallel impedance, ij, and the intensity that crosses the equivalent parallel impedance, i. The result of dividing member by member the equations of each impedance by the equivalent parallel impedance equation results

ij = 1Zj1Zparalelo⋅i

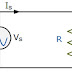
This expression shows that "the total current incoming to the set of impedances connected in parallel is divided among them inversely proportional to their value", that is why the circuit of figure 1 is known as an intensity divider.